Does Correlation Imply Causation After All? 1
Gregory Hill 2, Monash University
Extended Abstract
One of the most persistent untested maxims in the statistical sciences is "correlation does not imply causation". This adage is taught widely to students and practitioners, in order to prevent the logical fallacy of cum hoc ergo propter hoc ("with this, therefore because of this"). In short, it is the idea that a simple statistical correlation between factors is not sufficient to infer that a causal relationship exists. The argument is that such a result may be interesting but at best indicates further research is warranted before causality may be claimed. As Edward Tufte explains "Correlation is not causation but it sure is a hint."
This study examines this maxim through a rigorous meta-analysis of scientific articles published in Science, Nature and other leading journals, from 1970 to 2005 (see Appendix A). Articles were included in the meta-analysis if they cited both an estimate of correlation (in the form of the Pearson Product-Moment Correlation Co-efficient) and causation (as determined by the original researchers). Thresholds for statistical significance levels (alphas) and p-values were not used, as publication in these prestigious journals is sufficient to ensure the quality of results.
From the 7,234 articles in the catchment, 655 were selected for this study. Each article was classified as C (causation was found) or N (causation not found). The articles were then "binned" into twenty uniform intervals based on their Pearson's rho statistic: 0.00-0.05, 0.05-0.10, ..., 0.95-1.00. The following results were obtained, where rho is the independent variable, and the proportion finding causation (C/C+N) is the dependent variable.
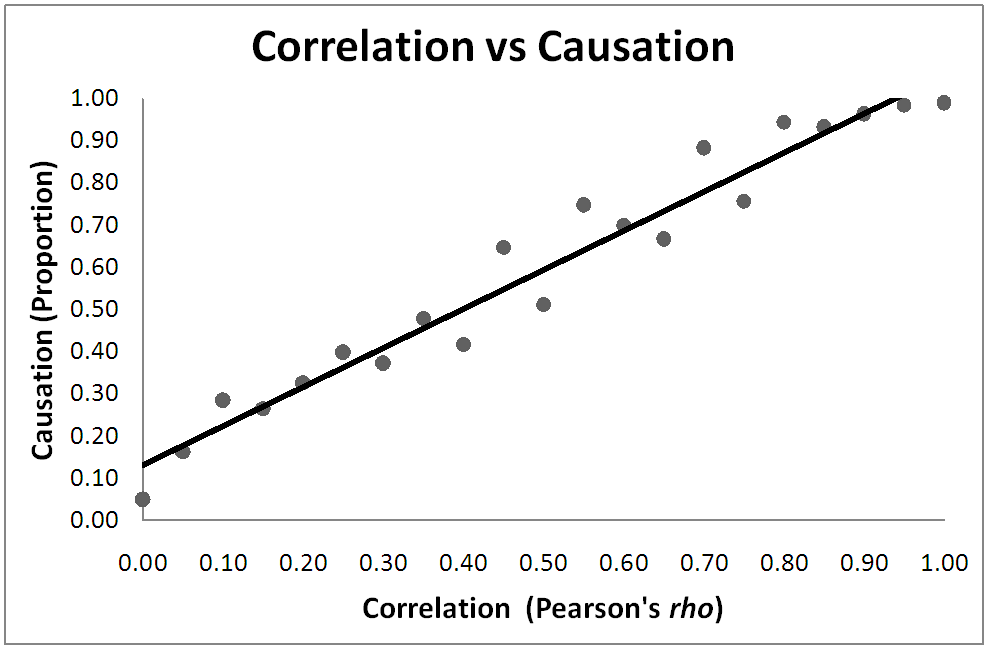
Note that the Pearson Product-Moment Correlation Co-efficient for this study is 0.977. With such a high correlation between the dependent and independent variables, it is reasonable to ask if we can infer causation here. Based on these results, we can, with over 98% studies with a rho of 0.977 attributing causation to the underlying variables.
However, the question of including this study in the meta-analysis arises. If we infer causality, then we should update the data point (for rho of 0.95-1.00) from 147/150 (98%) to 148/151 (98.01%). This would lend even more support for the case that correlation does in fact imply causation. To determine if the inclusion of a meta-analysis in itself is the usual scientific practice, we constructed an exhaustive list of all meta-analyses that don't list themselves (Appendix B). While the initial results were promising, a decision had to be made whether to include this study in the list or leave it out. Unable to resolve this, it is left as an open question for further research.
We examined the conventional statistical wisdom that "correlation does not imply causation" by conducting a rigorous meta-analysis of thousands of scientific articles. A high degree of correlation was found between the variables (Pearson's rho and causality), and based on the findings here, the adage is rejected: correlation does imply causation, statistically speaking.
1: Forthcoming in the International Journal of Observeration, Knowledge and Evidence, Vol. 27 (December, 2007)
2: Gregory Hill is a PhD candidate at Monash University, Melbourne, Australia. He has taught research methods (including statistics) and is interested in the philosophy of science.

This work is licensed under a
Creative Commons Attribution-ShareAlike 2.1 Australia License.